Pengfei Cui, Wanlin Guo

Journal of the Mechanics and Physics of Solids, 2022

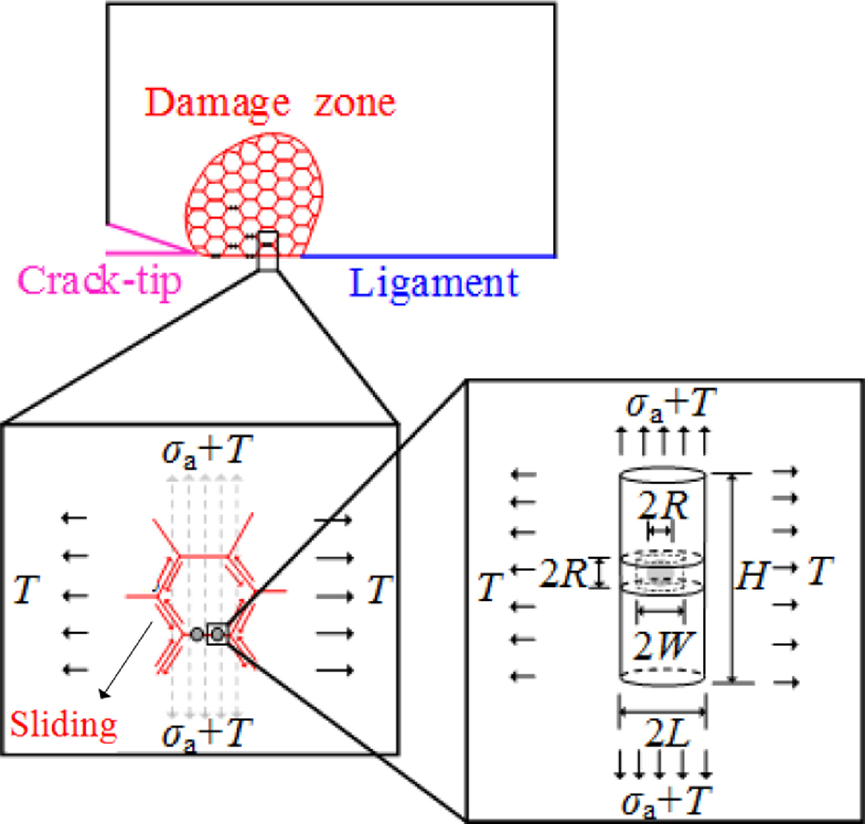
Abstract: Creep fracture mechanics has been extensively studied in the past half a century, but the gap between the creep crack-tip asymptotic field and crack growth prediction has not been effectively bridged so far, hindering the development of high temperature damage tolerance design. Here a predicting model is developed for three-dimensional crack growth in power-law creeping solids with the C(t)PC-Tz asymptotic solution being applied to quantify the creep crack growth driving force. The local resistance for creep crack growth in three-dimensional cracked structures is then described and evaluated based on the micro-cavity growth and constraint theories. Validation against forty-four crack growth experimental data for eleven creeping materials with deferent properties and specimen geometries and subjected to different load level in the literature shows that the proposed model can effectively predict the creep crack growth rate and provide the upper and lower limits. In all cases, the predicted crack growth life is within a triple error band around the experimental data. All the needed material parameters can be obtained from tension tests of standard uniaxial round bar specimens. Therefore, the proposed model can bridge the C(t)PC-Tz asymptotic solution with creep crack growth in practical materials and specimens, paving a road to predict damage tolerance of three-dimensional cracked structures at high temperature.

Link: https://www.sciencedirect.com/science/article/pii/S0022509622002113