ACS Nano., (2023) 

Abstract: 

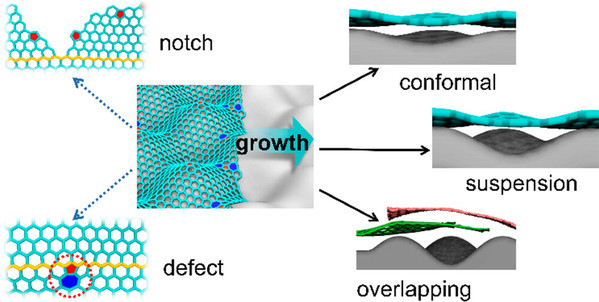
Chemical growth of two-dimensional (2D) materials with controlled morphology is critical to bring their tantalizing properties to fruition. However, the growth must be on a substrate, which involves either intrinsic or intentionally introduced undulation, at a scale significantly larger than the materials thickness. Recent theory and experiments showed that 2D materials grown on a curved feature on substrates can incur a variety of topological defects and grain boundaries. Using a Monte Carlo method, we herein show that 2D materials growing on periodically undulated substrates with nonzero Gaussian curvature of practical relevance follow three distinct modes: defect-free conformal, defect-free suspension and defective conformal modes. The growth on the non-Euclidean surface can accumulate tensile stress that gradually lifts the materials from substrates and progressively turns the conformal mode into a suspension mode with increasing the undulation amplitude. Further enhancing the undulation can trigger Asaro−Tiller−Grinfield growth instability in the materials, manifested as discretely distributed topological defects due to strong stress concentration. We rationalize these results by model analyses and establish a “phase” diagram for guiding the control of growth morphology via substrate patterning. The undulation-induced suspension of 2D materials can help understand the formation of overlapping grain boundaries, spotted quite often in experiments, and guide how to avoid them.

Link:  https://doi.org/10.1021/acsnano.3c00661