Pengfei Cui, Chongmin She, Rui Deng, Wanlin Guo.

International Journal of Solids and Structures, 279, 1 , 112370(2023)

Abstract: 

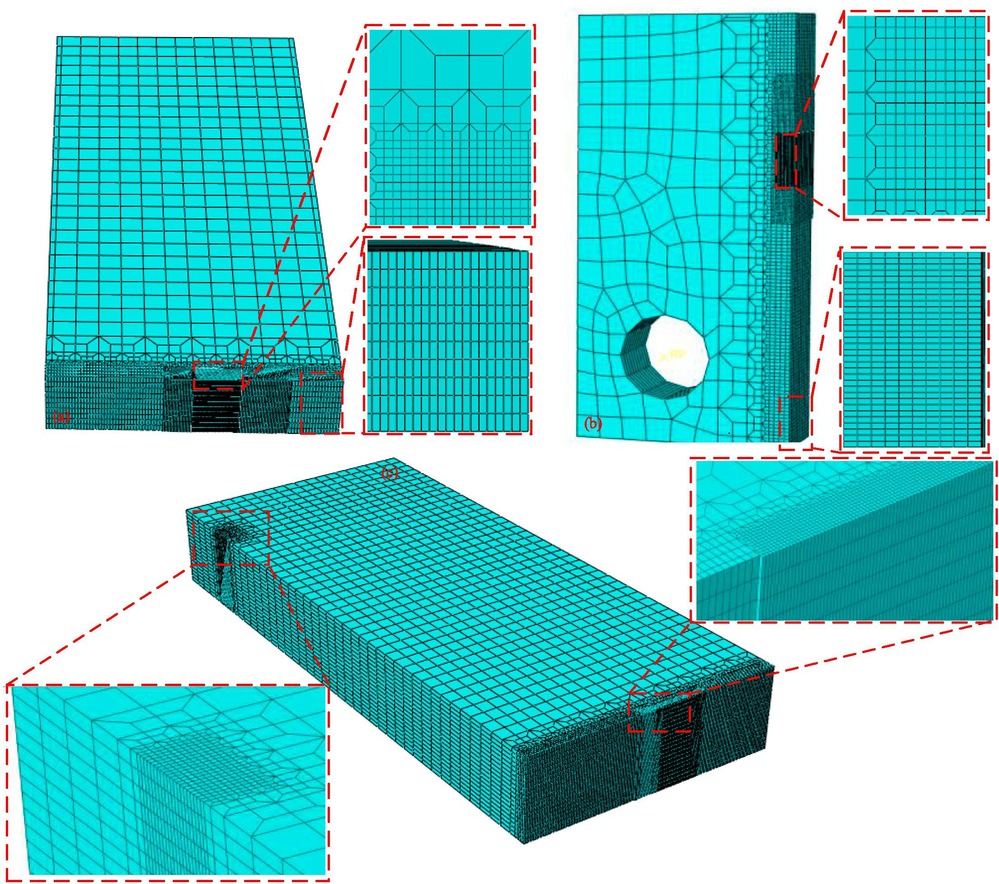
The crack-tip in-plane (Q and A2) and out-of-plane constraint (Tz) parameters have been extensively studied for ductile fracture problems on the basis of the pioneering HRR and J-Tz solutions. However, these analytic solutions rarely focus on the steady growing cracks, which play a vital role in J-R curve and integrity assessments of complicated structures. In this work, three-dimensional finite element method and GTN damage model are adopted to simulate quasi-static ductile crack growth under different plastic exponents, geometries and load levels. With the follow-up coordinate system, the J-Tz solution is extended to describe the crack-tip stress distributions of the quasi-static elastic–plastic growing cracks. It is found that in front of steady growth cracks, Tz strongly depends on specimen geometry. In the range of small-scale yielding, tensile stress and Tz gradually increase with increasing load J/JC. When the large-scale yielding stage is approaching, tensile stress and Tz tend towards a stable state. The maximum relative errors between the J-Tz solution and three-dimensional finite element results are 4.16% and 9.28% with J/JC smaller than 1 and 2, respectively. Such dominance and geometry independence of the leading order J-Tz solution make it more simply and effectively to assess the ductile fracture problems.

Link：https://doi.org/10.1016/j.ijsolstr.2023.112370